Wzory na pochodne funkcji

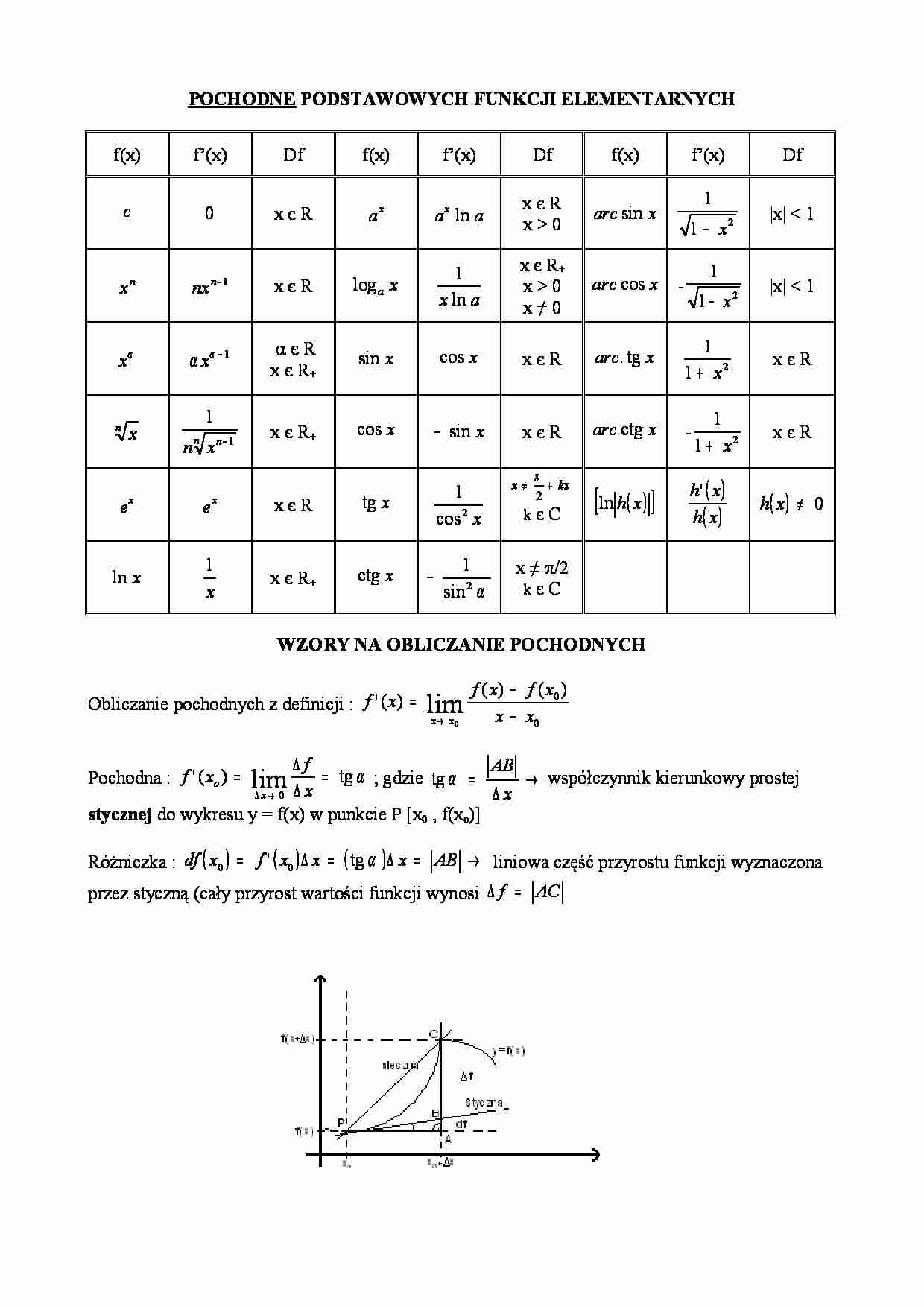
Pochodne funkcji są jednym z najważniejszych pojęć w matematyce.

Wraz z pochodnymi, można obliczyć tempo zmiany funkcji w danym punkcie oraz jej nachylenie w tym miejscu.

Jest to niezwykle przydatne narzędzie w wielu dziedzinach, takich jak fizyka, ekonomia czy inżynieria. W niniejszym artykule przyjrzymy się dokładniej wzorom na pochodne funkcji oraz wyjaśnimy, jak wykorzystać je w praktyce. Zanim przejdziemy do omawiania wzorów, warto zaznaczyć, że pochodna funkcji oznaczana jest symbolem f(x).

Oznacza to, że pochodna funkcji f w punkcie x jest równa pochodnej tej funkcji w danym punkcie. Innymi słowy, jest to pochodna funkcji w danym momencie.

Teraz przejdźmy do najważniejszych wzorów na pochodne funkcji. 1. Pochodna funkcji stałej. Pochodna funkcji stałej jest równa zero.

Zatem jeśli mamy funkcję f(x) = c, gdzie c jest stałą, to jej pochodna jest równa f(x) = 0. Jest to zrozumiałe, ponieważ funkcja stała nie zmienia się w żadnym punkcie, a więc jej tempo zmiany jest równe zero.

2.

Pochodna funkcji liniowej. Kolejnym ważnym wzorem jest pochodna funkcji liniowej. Funkcja liniowa ma postać f(x) = ax + b, gdzie a i b są stałymi. W tym przypadku pochodna jest równa f(x) = a.

Oznacza to, że nachylenie funkcji liniowej jest stałe i wynosi a. 3. Pochodna funkcji potęgowej.

Funkcja potęgowa jest postaci f(x) = x^n, gdzie n jest stałą. W tym przypadku pochodna jest równa f(x) = nx^(n-1). Na przykład, dla funkcji f(x) = x^2, pochodna wynosi f(x) = 2x.

4. Pochodna funkcji wykładniczej. Funkcja wykładnicza ma postać f(x) = e^x.

W tym przypadku pochodna jest równa f.